プログラミング（データ型・制御構造）【ITパスポート講座】

2020年2月26日2025年5月14日

この記事で学ぶこと

プログラミングの概要
データ型
制御構造

今回はITパスポートのプログラミングに関する内容に触れていきます。

くろん

プログラミング・・・聞いたことはあるけど書けるか不安だにゃ・・・

モナ

ITパスポートではプログラミングを書く問題は無くて、概要を押さえておくだけで大丈夫だニャ！

1. プログラム（プログラミング）とは
2. プログラミングの例題
3. プログラミングまとめ

プログラム（プログラミング）とは

コンピュータと言えばプログラミングと答える方も多いですが、このプログラミング(プログラム)は日常生活でも良く耳にします。

運動会や授業にもプログラムと言う言葉を用います。プログラムを直接和訳すると、予定の計画表や催し物の実行計画を書いた紙となります。

コンピュータにおけるプログラミングも、コンピュータに何をどういった手順で処理させるかと言った手順書です。

しかしコンピュータはディジタルとアナログのところでも触れた通り、0と1の世界で人間が直接あれしてこれしてと命令を出すのは困難です。

プログラミング言語

そのため人が扱えるようにするために厳密に文法を定め、それ通りに書いて初めてコンピュータ側が解釈して実行に移せるようになります。その文法をプログラム言語と呼びます。

言語と呼ぶだけあり、日本語や英語、ドイツ語と言ったようにプログラムの世界でも以下のように、いくつかのプログラミング言語があります。

プログラミング言語の例

C（シー）
C++（シープラスプラス）
C#（シーシャープ）
Java（ジャバ）
Python（パイソン）

キュー

これらは数あるプログラミング言語のうち、ほんの一部やで！

それぞれの言語により特徴や得意不得意が変わってくるので、何を開発するかによって言語を適切に選ぶことで効率的にプログラムを書くことが可能となります。

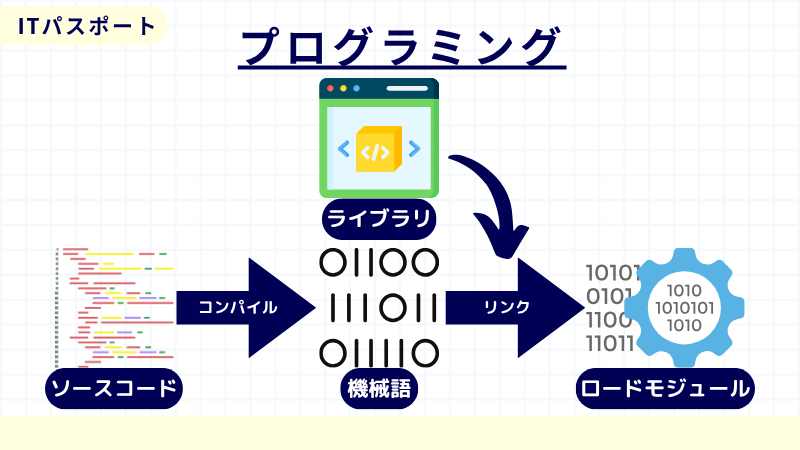
人が書いたプログラミング言語をソースコードと呼びます。ソースコードはコンピュータがそのまま理解することは難しく、コンピュータが理解できる文字（機械語）への変換が必要です。

人が書いたプログラムを機械語に置き換える翻訳ソフトはコンパイラと呼ばれ、コンパイラによって翻訳されることをコンパイルと呼びます。

コンパイラされた機械語に、ライブラリなどの必要なものを付け加えるリンクと呼ばれる処理をして初めて実行できます。

疑似言語

ITパスポートでは、CやJavaではなく疑似言語を用いた問題が出題されます。疑似言語とは、アルゴリズムを表現するための疑似的なプログラミング言語です。

疑似言語はPC上で実装できません。記述形式については、情報処理推進機構（IPA）を確認しておきましょう。

www.ipa.go.jp

https://www.ipa.go.jp/shiken/syllabus/ps6vr7000000i9dp-att/shiken_yougo_ver5_...

https://www.ipa.go.jp/shiken/syllabus/ps6vr7000000i9dp-att/shiken_yougo_ver5_0.pdf

関数

関数は、あらかじめ用意した処理に名前を付けたものです。手続と呼ぶケースもあります。関数はカッコの中に指定されたデータ（引数）を使って処理を行い、その結果の値（戻り値）を返します。

モナ

y=2x+1に、引数としてx=3を渡せば=7が返ってくるイメージだニャ！

データ型

変数には型があります。アルゴリズムの章において、変数はデータを入れる箱と解説しましたが、この箱に入るデータの種類をデータ型と呼びます。

代表的なデータ型と、データの具体例を確認しておきましょう。

データ型	データの具体例
整数型（int型など）	-5 , 0 , 150
実数型（float型・double型など）	-2.17 , 0.8 , 12.345
文字型（char型など）	“A” , “b”
論理型（bool型など）	true , false

制御構造

アルゴリズム同様、プログラミングも順次・選択・繰り返しの3つの構造で構成されています。

モナ

選択の場合、if,else ifなどの表現を使って分岐させるニャ！

if(条件式1) 　　処理1(条件式1成立時の処理) elseif(条件式2) 　　処理2(条件式1不成立　かつ　条件式2成立時の処理) else 　　処理3(条件式1不成立　かつ　条件式2不成立時の処理) endif

キュー

繰り返しでは、forやwhileが使われてるで

例えば、1から10まで順番に表示する処理は以下のとおりです。

i ← 1 while (i が　10 以下）を表示する　i を表示する　i ←　i + 1 endwhile

プログラミングの例題

実際に例題を解いて問題に慣れていきましょう。

問1

コンピュータに対する命令を，プログラム言語を用いて記述したものを何と呼ぶか。(H.29秋/問81)

ア：PINコード
イ：ソースコード
ウ：バイナリコード
エ：文字コード

（ログイン後回答すると、ここに前回の正誤情報が表示されます）

問1の正解を表示

イ

問1の解説を表示

ア：PINコード
⇒PINコードは、端末にログインする際に個人を識別し認証するために使用される番号のことです。誤りです。

イ：ソースコード
⇒ソースコードは、コンピュータに対する命令を、プログラム言語の文法に従い記述したテキストです。正解です。

ウ：バイナリコード
⇒バイナリコードは、命令をコンピュータが解釈できる2進数で表したものです。機械語とも呼ばれます。誤りです。

エ：文字コード
⇒文字コードは、コンピュータ上で使用される文字や記号を置き換えるためのコードです。ASCII・UTF8・EUC・Shift-JISなどがあります。

以上より、「イ」が正解です。

問2

4個の要素から成るデータの並びを，次の手順を繰り返して昇順に整列するとき，整列が終了するまでに(1)から(3)の一連の手順は，何回実行されるか。ここで，最初はデータの並び全体を整列対象とする。

データの並び：[27，42，33，12]

〔手順〕

整列対象中の要素の最大の値を選び，最後の要素と入れ替える。
最後の要素を整列対象から外す。
整列対象に要素が1個以上残っていれば，(1)から(3)の一連の手順を実行する。残っていなければ，整列完了なので終了する。

(R.7春/問98)

ア：2
イ：3
ウ：4
エ：5

（ログイン後回答すると、ここに前回の正誤情報が表示されます）

問2の正解を表示

ウ

問2の解説を表示

初期値の [27，42，33，12] に対して、(1)～(3)の処理を繰り返します。

【1回目】
最大の要素 42 を最後の要素 12 と入れ替えます。
[27，12，33，42] 最後の要素 42 を整列対象から外します。
[27，12，33，42] 整列対象の要素は3つなので、(1)に戻ります。

【2回目】
最大の要素 33 を最後の要素 33 と入れ替えます。ここでは変化しません。
[27，12，33，42] 最後の要素 33 を整列対象から外します。
[27，12，33，42] 整列対象の要素は2つなので、(1)に戻ります。

【3回目】
最大の要素 27 を最後の要素 12 と入れ替えます。
[12，27，33，42] 最後の要素 27 を整列対象から外します。
[12，27，33，42] 整列対象の要素は1つなので、(1)に戻ります。

【4回目】
最大の要素 12 を最後の要素 12 と入れ替えます。ここでは変化しません。
[12，27，33，42] 最後の要素 12 を整列対象から外します。
[12，27，33，42] 整列対象の要素はないので、整列は終了です。
以上より、整列終了までの繰返し回数は4回です。したがって「ウ」が正解です。

問3

関数 binaryToInteger は，1桁以上の符号なし2進数を文字列で表した値を引数 binaryStr で受け取り，その値を整数に変換した結果を戻り値とする。例えば，引数として”100″を受け取ると，4を返す。プログラム中のa，bに入れる字句の適切な組合せはどれか。

〔プログラム〕

ITパスポート令和6年春/問85

(R.6春/問85)

	a	b
ア	(2 の i乗) – 1	integerNUM × digitNUM × exponent
イ	(2 の i乗) – 1	integerNUM + digitNUM × exponent
ウ	2 の (i – 1)乗	integerNUM × digitNUM × exponent
エ	2 の (i – 1)乗	integerNUM + digitNUM × exponent

ア
イ
ウ
エ

（ログイン後回答すると、ここに前回の正誤情報が表示されます）

問3の正解を表示

エ

問3の解説を表示

2進数の各桁と10進数の対応関係を把握しておきましょう。

2進数	\(2^{0}\)	\(2^{1}\)	\(2^{2}\)	\(2^{3}\)	\(2^{4}\)	\(2^{5}\)	\(2^{6}\)	\(2^{7}\)
10進数	1	2	4	8	16	32	64	128

関数のfor文内では、引数 binaryStr の末尾から1文字ずつ順番に処理を行います。設問で例として挙げられている”100″であれば、以下のステップで4を返します。

STEPLIST

i=1　末尾からi番目は0 ⇒ 20×0＝0
i=2　末尾からi番目は0 ⇒ 21×0＝0
i=3　末尾からi番目は1 ⇒ 22×1＝4

したがって、20×0＋21×0＋22×1 を行うプログラムが正解です。

aについて

引数の文字列を2進数とすると、末尾から1桁目は0（＝20）、同2桁目は2（＝21）、同3桁目は4（＝22）です。

末尾からの位置と指数には「末尾からの位置－1＝指数」の関係があるため、指数部は i-1 と表せます。したがって、aは「2 の (i － 1)乗」が当てはまります。

bについて

戻り値の integerNum は、各桁の10進表現を合計したものです。したがって、bは「integerNUM + digitNUM × exponent」が当てはまります。

これより、適切な組合せは「エ」です。

問4

手続 printArray は，配列 integerArray の要素を並べ替えて出力する。手続 printArray を呼び出したときの出力はどれか。ここで，配列の要素番号は1から始まる。

〔プログラム〕
ITパスポート令和5年春/問60

(R.5春/問60)

ア：1，2，3，4
イ：1，3，2，4
ウ：3，1，4，2
エ：4，3，2，1

（ログイン後回答すると、ここに前回の正誤情報が表示されます）

問4の正解を表示

ア

問4の解説を表示

プログラムをたどってみましょう。

integerArray = {2, 4, 1, 3}
integerArrayの要素数 = 4
nを1から 4 – 1 = 3 まで繰り返します。

〔n = 1 のループ処理〕
mを1から 4 – 1 = 3 まで繰り返します。
integerArray[1] = 2、integerArray[2] = 4
2＞4 は false なので、何も処理しません。
integerArray[2] = 4、integerArray[3] = 1
4＞1 は true なので、2つの位置を入れ替えます。
⇒integerArray = {2, 1, 4, 3}
integerArray[3] = 4、integerArray[4] = 3
4＞3 は true なので、2つの位置を入れ替えます。
⇒integerArray = {2, 1, 3, 4}

〔n = 2 のループ処理〕

mを1から 4 – 2 = 2 まで繰り返します。
integerArray[1] = 2、integerArray[2] = 1
2＞1 は true なので、2つの位置を入れ替えます。
⇒integerArray = {1, 2, 3, 4}
integerArray[2] = 2、integerArray[3] = 3
2＞3 は false なので、何も処理しません。

〔n = 3 のループ処理〕

mを1から 4 – 3 = 1 まで繰り返します。
integerArray[1] = 1、integerArray[2] = 2
1＞2 はfalseなので、何も処理しません。
ループ処理が終了した時点で、配列 integerArray の要素は {1, 2, 3, 4} なので、先頭から順に出力すると「1, 2, 3, 4」が出力されます。

したがって「ア」が正解です。

問5

配列に格納されているデータを探索するときの，探索アルゴリズムに関する記述のうち，適切なものはどれか。(R.5春/問69)

ア：2分探索法は，探索対象となる配列の先頭の要素から順に探索する。
イ：線形探索法で探索するのに必要な計算量は，探索対象となる配列の要素数に比例する。
ウ：線形探索法を用いるためには，探索対象となる配列の要素は要素の値で昇順又は降順にソートされている必要がある。
エ：探索対象となる配列が同一であれば，探索に必要な計算量は探索する値によらず，2分探索法が線形探索法よりも少ない。

（ログイン後回答すると、ここに前回の正誤情報が表示されます）

問5の正解を表示

イ

問5の解説を表示

探索アルゴリズムは、データ群の中から目的のデータを探し出すアルゴリズムです。代表的な探索アルゴリズムは、線形探索法・2分探索法・ハッシュ法です。

線形探索法

データ群の先頭から1つずつ順に値を比較していく方法です。データ群が整列されていなくても探索できますが、平均比較回数はデータの総数の半分なので、探索効率は悪くなります。

2分探索法

要素が昇順または降順に整列されたデータ群に対して、探索範囲を2分の1に狭めることを繰り返して目的のデータを探索する方法です。効率よく目的のデータを探せます。

ハッシュ法

目的のデータの探索キーをハッシュ関数にかけて、データの格納位置を直接計算する方法です。基本的に1回の探索で目的の値にたどり着けます。

ア：2分探索法は，探索対象となる配列の先頭の要素から順に探索する。
⇒配列の先頭の要素から順に探索する方法は線形探索法です。2分探索法は、
「探索範囲の中央に位置する値と比較する」「探索範囲を2分の1に狭める」を繰り返して探索する方法です。

イ：線形探索法で探索するのに必要な計算量は，探索対象となる配列の要素数に比例する。
⇒要素がN個のデータ群から線形探索法で探すとき、目的のデータが1番最初にあれば1回、最後にあればN回の比較が必要な探索方法です。どこに目的のデータがあるかはランダムなので、線形探索法の平均比較回数は\frac{N－1}{2}回（データ総数の約半分）です。データ群が多いほど、平均比較回数も増えます。正解です。

ウ：線形探索法を用いるためには，探索対象となる配列の要素は要素の値で昇順又は降順にソートされている必要がある。
⇒線形探索法のデータ群は整列されている必要はありません。データ群をあらかじめ整列しておく必要があるのは2分探索法です。

エ：探索対象となる配列が同一であれば，探索に必要な計算量は探索する値によらず，2分探索法が線形探索法よりも少ない。
⇒探索対象が同一の場合、2分探索法は線形探索法よりも平均比較回数が少なくなります。平均比較回数のため、データの並び方次第では探索する値によっては線形探索法のほうが少ない計算量で探索できる場合もあります。また、2分探索法は事前に整列しておく必要があるため、計算量が必要なケースでは効率が悪化しがちです。

以上より、「イ」が正解です。