[SPI・数学]集合:積集合[無料問題集]

今回はSPIにおける積集合を確認していきましょう。

AにもBにもCにも該当するような範囲を見つけろって言われてもなかなかわからねぇ・・・!

積集合もベン図を書けば楽勝!
SPI積集合の例題
今回は扱う集合の数が増え、\(3\)つの集合の場合のベン図を見ていきます。
ベン図が3つ、4つと増えても根本的な考え方は変わりません。
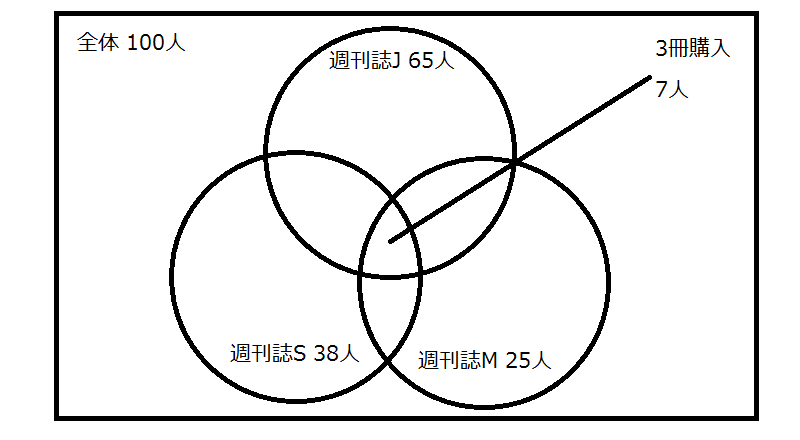
問題
高校生\(100\)人を対象に、週刊誌J、S、Mそれぞれの購読状況をアンケートした結果、以下のようになった。
週刊誌Jを購読している人:65人
週刊誌Sを購読している人:38人
週刊誌Mを購読している人:25人
ここで、J、S、Mをいずれも購読していない人はいなかった。
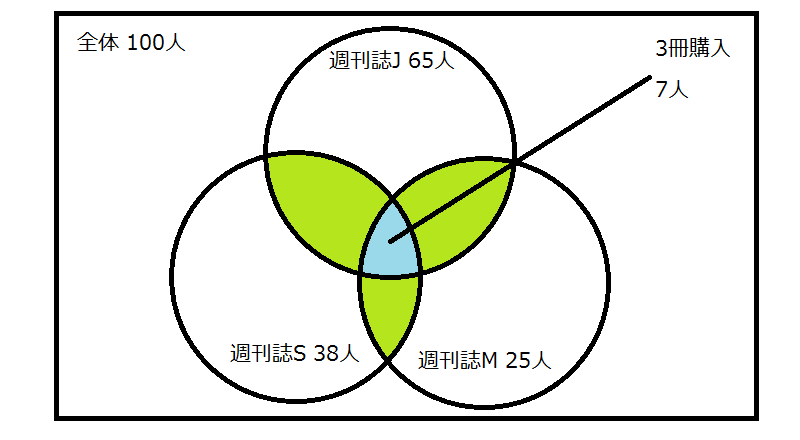
3冊の週刊誌を購読している人が7人いた場合、2冊以上の週刊誌を購読している人は何人いるか。
人
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
スポンサーリンク
SPI積集合のまとめ
今回はベン図が3つの場合を扱いました。
ベン図の数が増えてくると複雑になり解きづらく感じるかもしれませんが、やることはベン図が2つのときとなんら変わりはありません。
この問題で躓いた場合はまず、和集合・積集合の求め方をしっかり復習した上でもう一度問題にチャレンジしてみましょう。

ベン図はほんと便利やで~






ディスカッション
コメント一覧
まだ、コメントがありません