[SPI・数学]図表：二つの表[無料問題集]
今回はSPIにおける二つの表の問題を確認していきましょう。
SPI二つの表の例題
二つの表を扱う問題は、SIPの中でも難易度が高めです。
それぞれの表がどのように関連しているか見抜く力が求められます。
問題1
表1は出身国(日本・アメリカ・中国・ロシアのいずれか)に基づいて大学ごとの割合を示したものである。また、表2は大学ごとの学生数が全体の学生数に占める割合を表している。
<表1>
| A | B | C | D | 四つの合計 | |
| 日本 | 20% | 35% | 25% | 40% | |
| アメリカ | 60% | 20% | 15% | 30.25% | |
| 中国 | 5% | 15% | 35% | 20% | 17.75% |
| ロシア | 15% | 30% | 25% | ||
| 計 | 100% | 100% | 100% | 100% | 100% |
<表2>
| 大学 | A | B | C | D | 計 |
| 学生数の割合 | 30% | 15% | 20% | 35% | 100% |
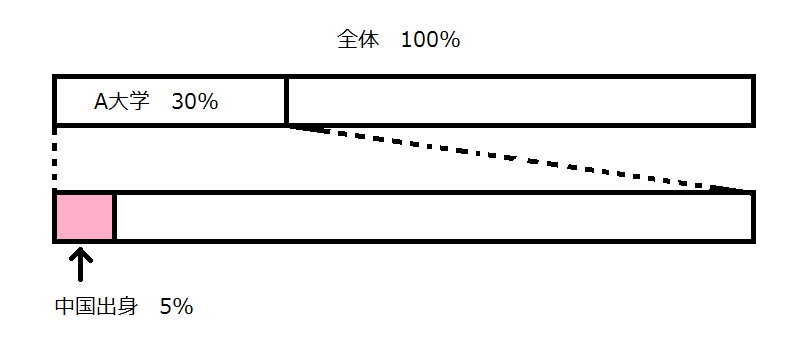
大学Aに通う学生の内、中国出身の学生は四つの大学での学生数全体の何%か。
%
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
<表2>
| 大学 | A | B | C | D | 計 |
| 学生数の割合 | 30% | 15% | 20% | 35% | 100% |
表2を見ると全体の30%がA大学の学生と分かります。
次に表1から、Aの中国出身の割合を見ます。
<表1>
| A | B | C | D | 四つの合計 | |
| 日本 | 20% | 35% | 25% | 40% | |
| アメリカ | 60% | 20% | 15% | 30.25% | |
| 中国 | 5% | 15% | 35% | 20% | 17.75% |
| ロシア | 15% | 30% | 25% | ||
| 計 | 100% | 100% | 100% | 100% | 100% |
この値を掛け算すればよいので、以下のような式が立てられます。
\[30\% \times 5\% = 1.5\%\]
したがって1.5%が答えとなります。
問題2
表1は出身国(日本・アメリカ・中国・ロシアのいずれか)に基づいて大学ごとの割合を示したものである。
また、表2は大学ごとの学生数が全体の学生数に占める割合を表している。
<表1>
| A | B | C | D | 四つの合計 | |
| 日本 | 20% | 35% | 25% | 40% | |
| アメリカ | 60% | 20% | 15% | 30.25% | |
| 中国 | 5% | 15% | 35% | 20% | 17.75% |
| ロシア | 15% | 30% | 25% | ||
| 計 | 100% | 100% | 100% | 100% | 100% |
<表2>
| 大学 | A | B | C | D | 計 |
| 学生数の割合 | 30% | 15% | 20% | 35% | 100% |
D大学の日本出身の学生の人数はB大学の日本出身の学生の人数の何倍か。
小数が出る場合は小数第二位を四捨五入して求めよ。
倍
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題3
表1は出身国(日本・アメリカ・中国・ロシアのいずれか)に基づいて大学ごとの割合を示したものである。
また、表2は大学ごとの学生数が全体の学生数に占める割合を表している。
<表1>
| A | B | C | D | 四つの合計 | |
| 日本 | 20% | 35% | 25% | 40% | |
| アメリカ | 60% | 20% | 15% | 30.25% | |
| 中国 | 5% | 15% | 35% | 20% | 17.75% |
| ロシア | 15% | 30% | 25% | ||
| 計 | 100% | 100% | 100% | 100% | 100% |
<表2>
| 大学 | A | B | C | D | 計 |
| 学生数の割合 | 30% | 15% | 20% | 35% | 100% |
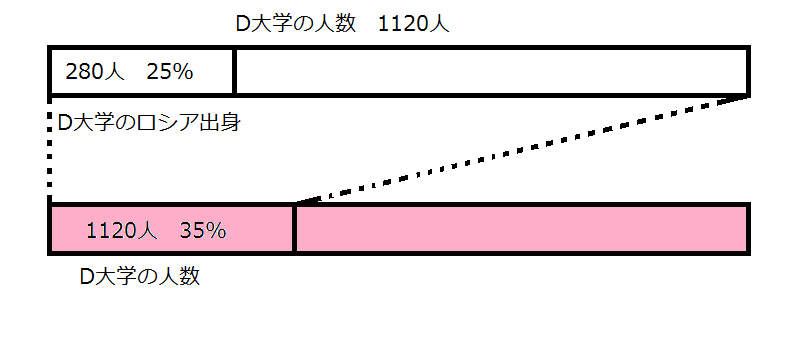
D大学のロシア出身の学生の人数は280人だった。
このとき四つの大学の全体の人数は何人か。
人
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
今までは表2を使ってから表1を使うことで、全体から個々の割合を求めてきました。
今回はその逆で、表1から表2を使うことで個々の数値から全体の数値を求めます。
まず表1より、D大学の学生全員の数を求めます。
<表1>
| A | B | C | D | 四つの合計 | |
| 日本 | 20% | 35% | 25% | 40% | |
| アメリカ | 60% | 20% | 15% | 30.25% | |
| 中国 | 5% | 15% | 35% | 20% | 17.75% |
| ロシア | 15% | 30% | 25% | ||
| 計 | 100% | 100% | 100% | 100% | 100% |
D大学全体の人数は「D大学のロシア出身の学生の人数」を「D大学のロシア出身の学生の割合」で割ることで算出できるので、以下のように立式できます。
\[280\verb|(人)| ÷ 25\% = 1120\verb|(人)|\]
したがって、D大学全体の人数は1,120人となります。
次に、表2より、四つの大学の学生全員の数を求めます。
<表2>
| 大学 | A | B | C | D | 計 |
| 学生数の割合 | 30% | 15% | 20% | 35% | 100% |
四つの大学全体の人数は「D大学全体の人数」を「四つの大学の人数の内、D大学の占める人数の割合」で割ることで算出できるので、以下の式で求まります。
\[1120\verb|(人)| ÷ 35\% = 3200\verb|(人)|\]
よって四つの大学全体の人数は、3,200人となります。
問題4
表1は出身国(日本・アメリカ・中国・ロシアのいずれか)に基づいて大学ごとの割合を示したものである。
また、表2は大学ごとの学生数が全体の学生数に占める割合を表している。
<表1>
| A | B | C | D | 四つの合計 | |
| 日本 | 20% | 35% | 25% | 40% | |
| アメリカ | 60% | 20% | 15% | 30.25% | |
| 中国 | 5% | 15% | 35% | 20% | 17.75% |
| ロシア | 15% | 30% | 25% | ||
| 計 | 100% | 100% | 100% | 100% | 100% |
<表2>
| 大学 | A | B | C | D | 計 |
| 学生数の割合 | 30% | 15% | 20% | 35% | 100% |
C大学におけるアメリカ出身の学生の割合は何％か。
%
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
SPI二つの表のまとめ
百分率だけでの計算が慣れない場合、仮に人数を当てはめてみると分かりやすいです。
例えば問1で、全体を1,000人とします。するとA大学の生徒数は30%なので300人、そのうち中国出身の学生は5%なので15人となります。
全体が1,000人の中、中国出身のA大学生は15人なので、\(15 ÷ 1000 = 0.015 =1.5\%\)といった具合に算出することも可能です。
福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
職歴：経理4年/インフラ・アプリエンジニア9年(内4年は兼務)/ライター7年
保有資格：簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断士 など
