[SPI・数学]対策問題(集合)～補集合～

• 1. 例題1
  • 1.1. 問題1

解説(クリックで展開)

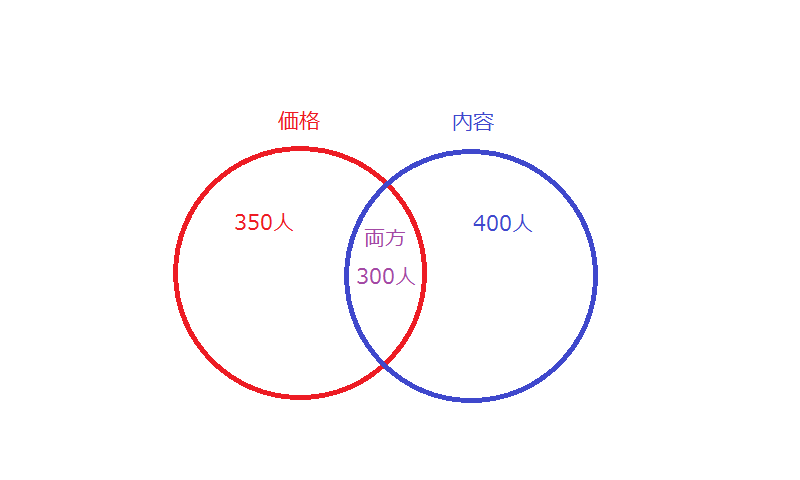
まずは表から得られた結果と、問題文からそれぞれに満足した人をベン図に表してみましょう。

求めたいのは「価格」も「内容」も不満足と答えた人で、ここで表されているベン図は「価格」と「内容」のうち、少なくとも一方には満足していると答えた人の人数です。

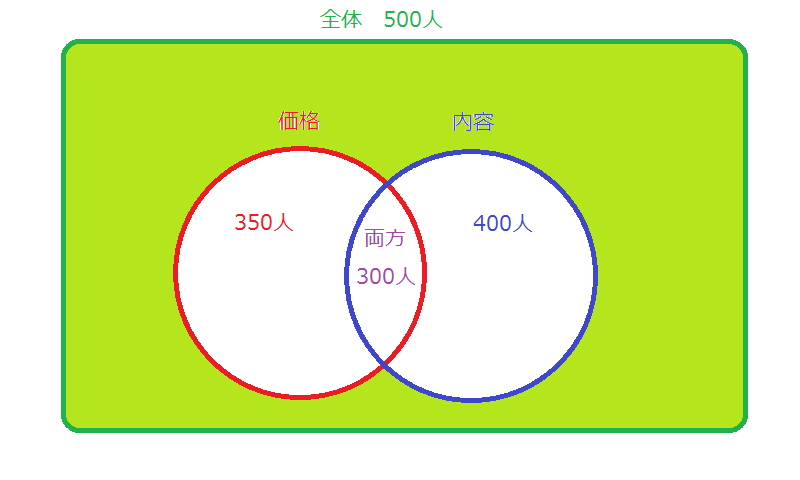
したがって、両方不満足と答えた人はベン図の外側を表しており、全体で\(500\)人と分かっているので、以下のようにベン図を書き足せば答えが見えてきます。

この黄緑色で塗りつぶした場所がどちらも不満足していた人の人数で、求めたい答えとなってくるので、「価格」が満足と答えた人と、「内容」が満足と答えた人の合計を求め、ダブってしまっている「両方」満足したと答えた人の人数を引くことで、少なくとも一方満足と答えている人の人数を求めることができます。

全体から求めた少なくとも一方満足と答えている人の人数を引くことで、「両方」不満足だった人の人数を求めることができます。

よって、答えは\(50\)人となります。

解答(クリックで展開)