[SPI・数学]組み合わせ:円順列[無料問題集]

今回はSPIの円順列に関する問題を確認していきましょう。


SPI円順列の例題
円順列は別名・数珠(じゅず)順列とも呼ばれます。
基本的には一部を固定すれば良いのですが、問題文の条件により計算方法が変わってきます。問題をよく読んで回答してください。
問題1
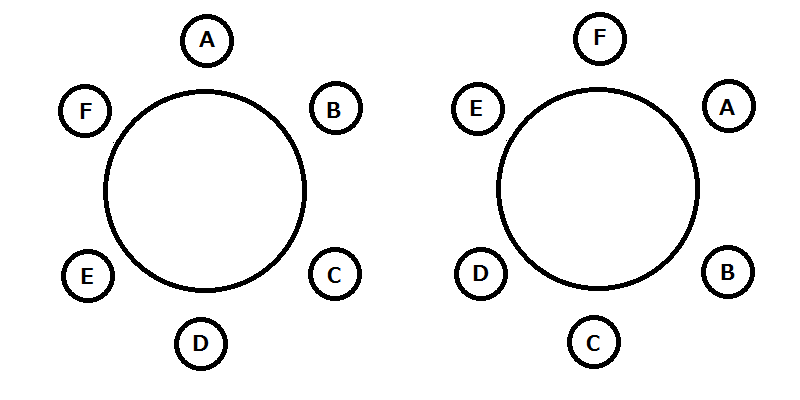
テーブルに番号が振られているとき、その座り方は何通りあるか。
通り
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題2
テーブルに番号が振られていないとき、その座り方は何通りあるか。
通り
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題3
テーブルに番号が振られておらず、BとCは必ず隣り合わせに座るとする。その座り方は何通りあるか。
通り
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題4
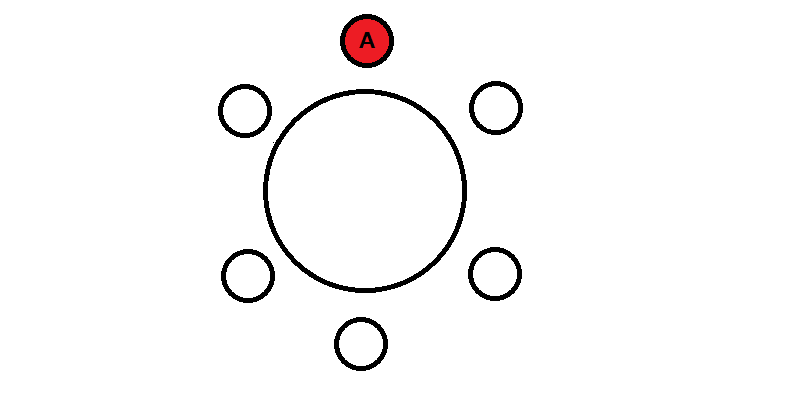
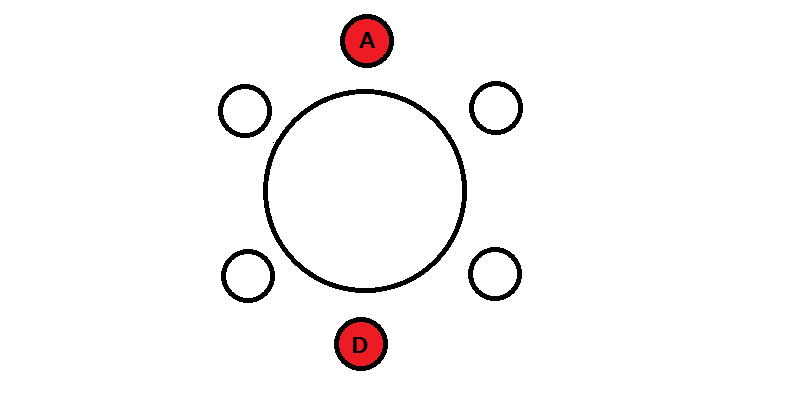
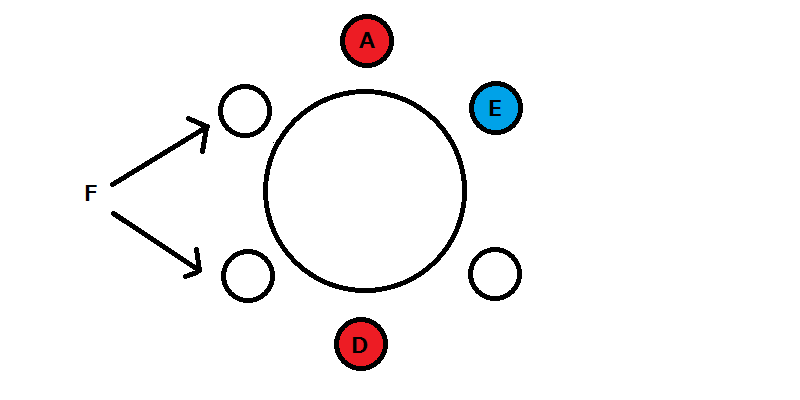
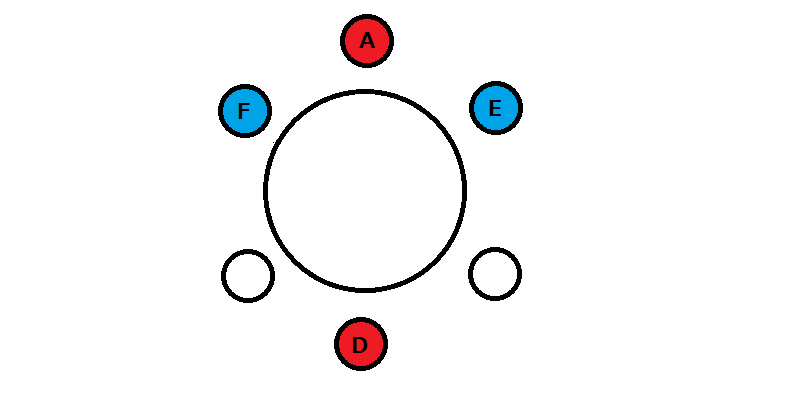
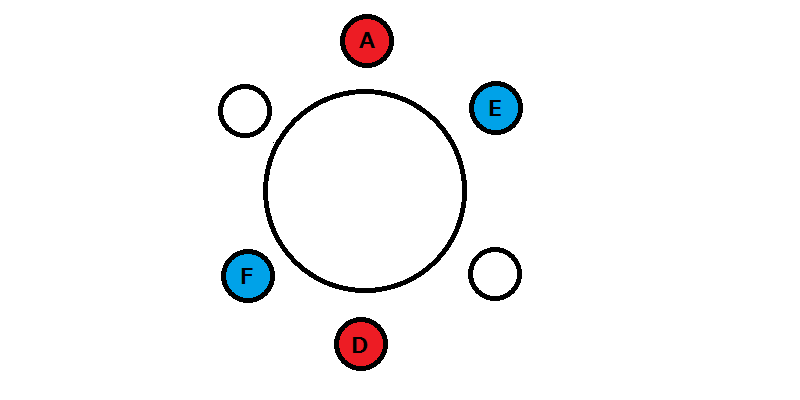
A、B、C、D、E、Fの6人がテーブルに座るとする。
テーブルに番号が振られておらず、AとDは向かい合って座るものとする。また、EとFは隣り合わせにならない場合、その座り方は何通りあるか。
通り
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
SPI円順列のまとめ
円順列ではどこかを固定するといった考え方が重要になってきます。
また、条件が増えれば増えるほど、計算の複雑さは増しますが、条件があるものを先に決めていくことで、かなり候補を少なく絞ることができ、計算が楽になります。

福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
職歴:経理4年/インフラ・アプリエンジニア9年(内4年は兼務)/ライター7年
保有資格:簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断士 など





ディスカッション
コメント一覧
まだ、コメントがありません