[SPI・数学]推論:条件[無料問題集]

今回はSPIにおける条件の問題を確認していきましょう。


SPI条件の例題
SPIの条件に関する問題は問いに対して、どの条件を加えれば答えられるようになるかを問われるパターンと、条件から数値を求めるパターンがあります。
それぞれを例題を通して見てみましょう。
問題1-1
(問い)
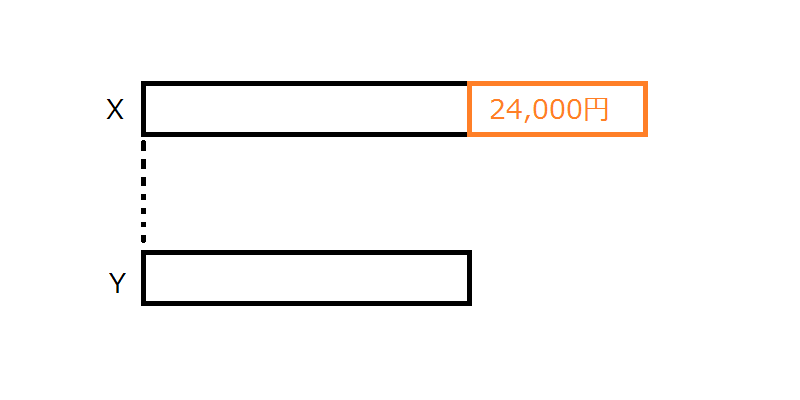
ある商品PとAがあり、価格の差は24,000円である。Aの価格はいくらか。
ア:PとAの価格を足すと88,000円である。
イ:Aの価格のほうが安い。
アのみ
イのみ
アとイの両方
両方あっても分からない
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題1-2
(問い)
1から6までの目のあるサイコロを2回振ったところ和は7であった。出た目はそれぞれいくつか。
ア:「2つのサイコロの積」の約数の数は4つであった。
イ:「2つのサイコロの差」の約数の数は2つであった。
アのみ
イのみ
アとイの両方
両方あっても分からない
(ログイン後回答すると、ここに前回の正誤情報が表示されます)

問題2-1
空欄に当てはまる数値を答えなさい。
X、Y、Zの3人のテストの平均点数は60点で、X、Y、Zの順に点数が高い。また、3人の点数について以下のことが分かっている。
ア:XとZの点数差はYの点数と等しい。
イ:YとZの点数差は20点である。
このとき、Xは[]点であった。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題2-2
空欄に当てはまる数値を答えなさい。
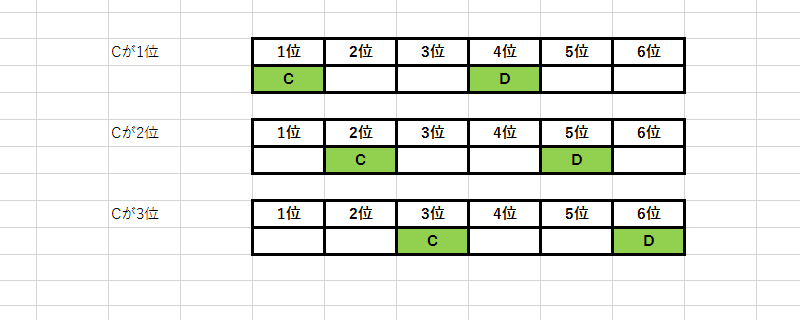
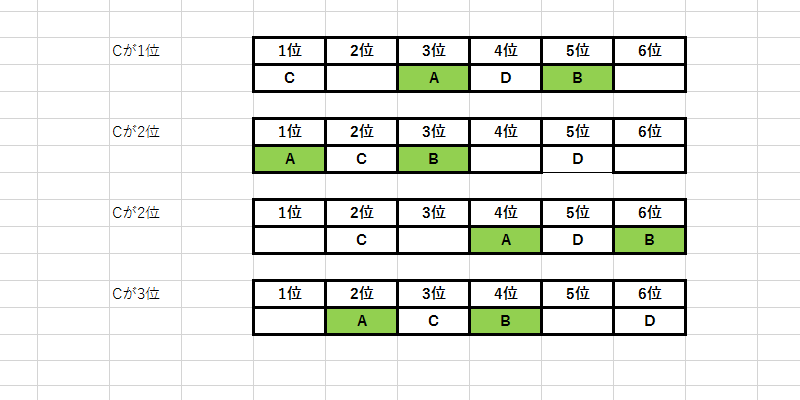
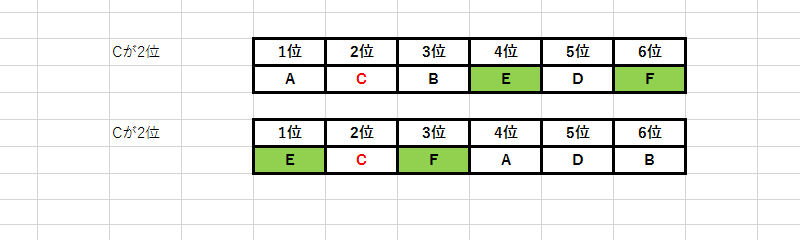
A、B、C、D、E、Fの6人でマラソンを行った、その結果について次のことが分かっている。
ア:AはBより順位が2位上である。
イ:CはDより順位が3位上である。
ウ:EはFより順位が2位上である。
このときCは[]位である。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題2-3
ア:3人の平均点は350点だった。
イ:Zの点数は300点だった。
このとき、Yの点数は最も高くて[]点である。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
SPI条件のまとめ
数値を求める問題では、候補をどのように絞り込み、短い時間で求められるかが重要です。
表に書き出す方法や式にして範囲を狭める方法など手法はさまざまなので、より多くの問題を解いてパターンに慣れていきましょう。

福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
経理4年/インフラエンジニア7年(内4年は兼務)/ライター5年(副業)
簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断修得者 など





ディスカッション
コメント一覧
まだ、コメントがありません