[SPI・数学]推論:分類[無料問題集]

今回はSPIにおける分類の問題を確認していきましょう。


SPI分類の例題
SPIにおける分類の問題では、主に3つ以上の対象物があります。
その合計やお互いの関係性を提示し、それに条件を加えることで範囲を絞っていくことが正解を導く正しい手順です。
条件がいくつもあり混乱してしまいそうですが、パターンを覚えてしまえば簡単なので是非対策してください。
では、例題を見てみましょう。
問題1-1
Ⅰ)3種類とも、少なくても1本は咲いている。
Ⅱ)菊の本数は、薔薇の本数よりも少ない。
次の推論ア、イ、ウのうち、必ず正しいといえるものはどれか、全て選べ。
ア:ユリが2本なら、菊は3本である。
イ:ユリが4本なら、菊は2本である。
ウ:ユリが5本なら、菊は1本である。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題1-2
Ⅰ)3種類とも、少なくても1本は咲いている。
Ⅱ)菊の本数は、薔薇の本数よりも少ない。
次の推論カ、キ、クのうち、必ず正しいといえるものはどれか、全て選べ。
カ:菊とユリが同じ本数なら、薔薇は5本である。
キ:薔薇とユリが同じ本数なら、菊は1本である。
ク:ユリが薔薇より2本以上多いなら、菊は1本である。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)

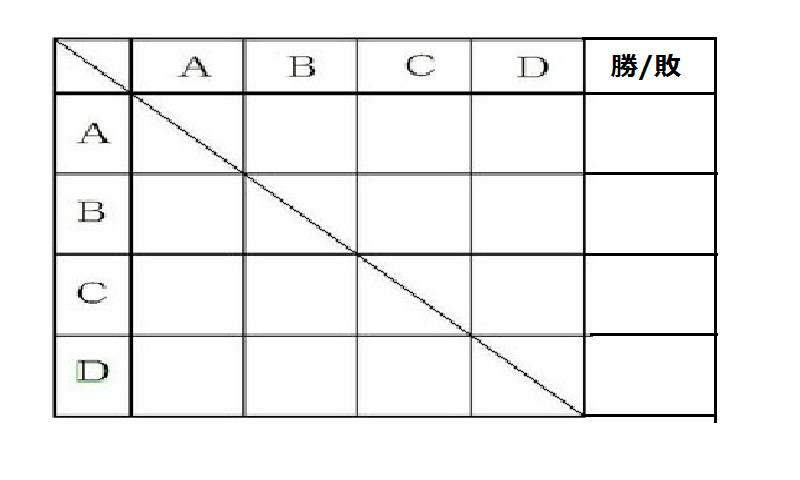
問題2-1
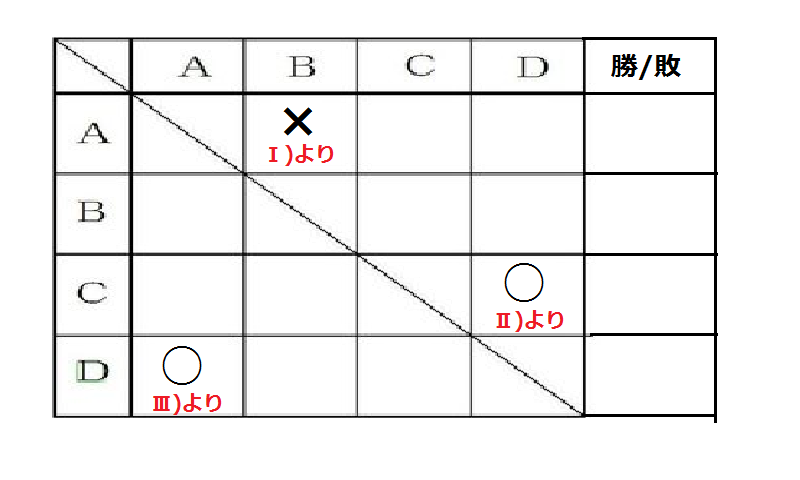
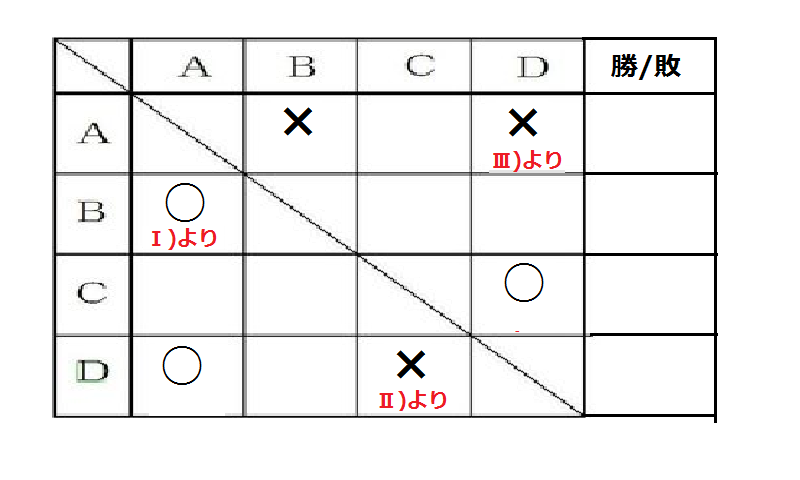
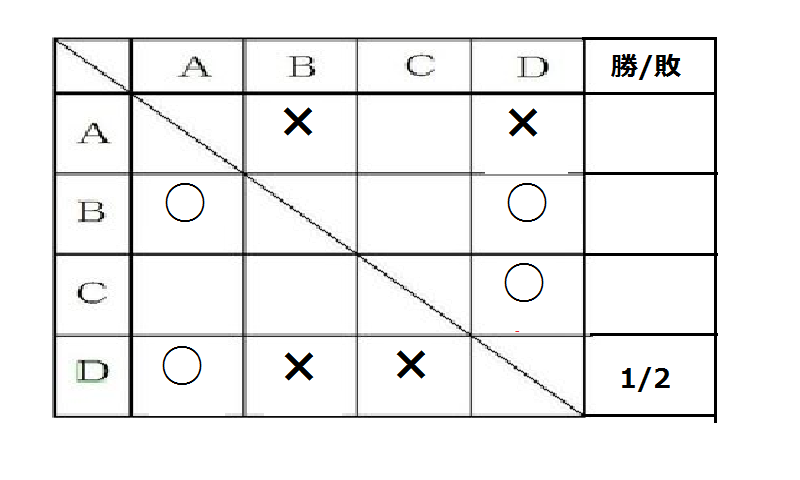
Ⅰ)AはBに負けた。
Ⅱ)CはDに勝った。
Ⅲ)DはAに勝った。
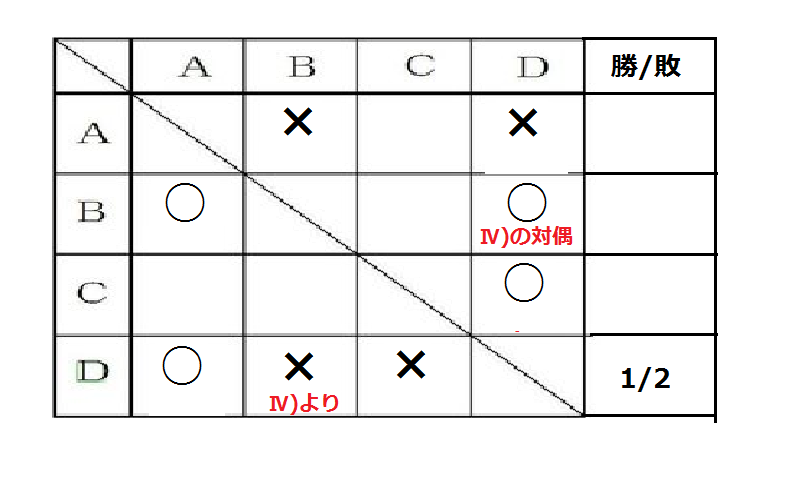
Ⅳ)Dは1勝しかできなかった。
上記の条件だけで結果が全て分かるのは誰か、全員選べ。
A
B
C
D
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
問題2-2
Ⅰ)AはBに負けた。
Ⅱ)CはDに勝った。
Ⅲ)DはAに勝った。
Ⅳ)Dは1勝しかできなかった。
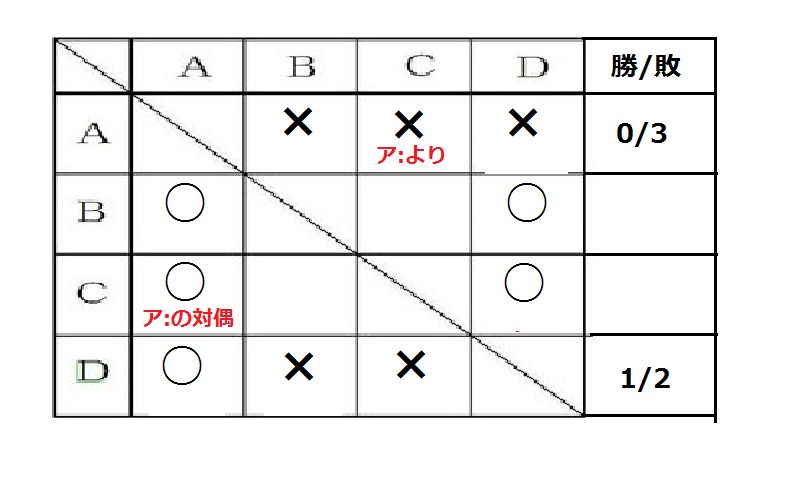
Ⅰ)~Ⅳ)の他に、次のア、イ、ウのうち、少なくともどの情報が加われば4人の結果が全て分かるか。全て選べ。
ア:3戦とも負けた人がいた。
イ:3戦とも勝った人がいた。
ウ:BはCに勝った。
(ログイン後回答すると、ここに前回の正誤情報が表示されます)
SPI分類のまとめ
実際に図や表を書けば分かるのですが、実際の試験では時間が限られています。
より早く正確に書くことを求められるので、何度も練習を重ねて書き方をマスターしていきましょう。


福井県産。北海道に行ったり新潟に行ったりと、雪国を旅してます。
経理4年/インフラエンジニア7年(内4年は兼務)/ライター5年(副業)
簿記2級/FP2級/応用情報技術者/情報処理安全確保支援士/中小企業診断修得者 など









ディスカッション
コメント一覧
まだ、コメントがありません